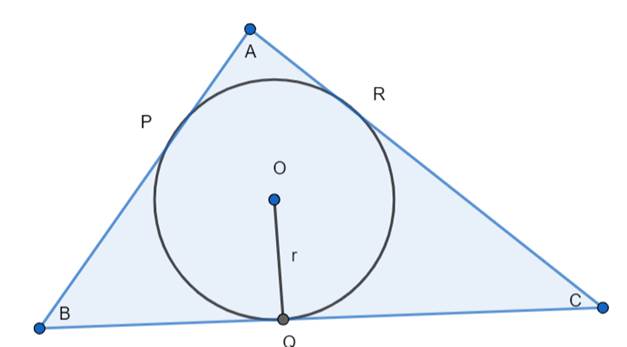
In the figure shown below, the sides AB, BC and CA of a triangle ABC touch a circle with centre O and radius ‘r’ at P, Q and R respectively. Prove that:

(i) AB + CQ = AC + BQ

(ii) Area(ΔABC) = 1/2 (Perimeter of ΔABC) × r

(i) Theorem: The lengths of tangents drawn from an external point to a circle are equal.

Therefore,

AP = AR

BP = BQ

CQ = CR

AB + CQ = AP + BP + CQ

AB + CQ = AR + BP + CR

AB + CQ = (AR + CR) + BP

AB + CQ = AC + CQ

Hence, Proved.

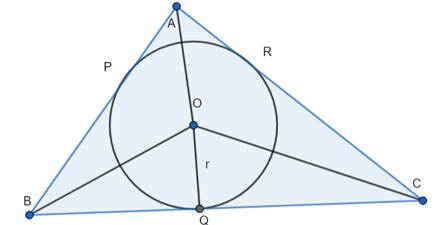
(ii) Joining OA, OB and OC, we get,

Area of ΔABC = Area of ΔOBC + Area of ΔOAB + Area of ΔOAC

= 1/2 (BC × OQ) + 1/2 (AB × OP) + 1/2 (AC × OR)

= 1/2 (BC × r) + 1/2 (AB × r) + 1/2 (AC × r)

= 1/2 (AB + BC + AC) × r

Area of ΔABC = 1/2 (Perimeter of ΔABC) × r

Hence, Proved.