In Fig. 9.42, side BC of Δ ABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.

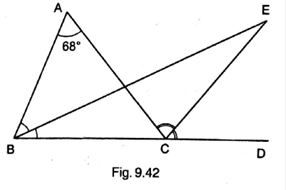
By exterior angle theorem,

∠ACD = ∠A + ∠B

∠ACD = 68^o + ∠B

∠ACD = 34^o + ∠B

34^o = ∠ACD - ∠EBC (i)

Now,

In

∠ECD = ∠EBC + ∠E

∠E = ∠ECD - ∠EBC

∠E = ∠ACD - ∠EBC (ii)

From (i) and (ii), we get

∠E = 34^o