In Fig. 10.22, the sides BA and CA have been produced such that BA = AD and CA = AE. Prove that segment DE||BC.

Question

In Fig. 10.22, the sides BA and CA have been produced such that BA = AD and CA = AE . Prove that segment DE || BC .

Philoid · Accepted Answer

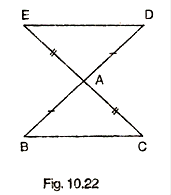
Given,

The sides BA and CA have been produced, such that:

BA = AD

And, CA = AE

We have to prove that,

DE ‖ BC

Consider and , we have

BA = AD and CA = AE (Given)

∠BAC = ∠DAE (Vertically opposite angle)

So, by SAS congruence rule we have:

Therefore, BC = DE and

∠DEA = ∠BCA,

∠EDA = ∠CBA (By c.p.c.t)

Now, DE and BC are two lines intersected by a transversal DB such that,

∠DEA = ∠BCA,

i.e., Alternate angles are equal

Therefore, DE BC