Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.

Question

Two lines AB and CD intersect at O such that BC is equal and parallel to AD . Prove that the lines AB and CD bisect at O .

Philoid · Accepted Answer

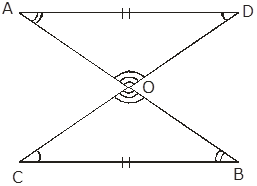
Given that,

Lines AB and CD intersect at O such that:

BC ‖ AD

And, BC = AD (i)

To prove: AB and CD bisect at O

Proof: In Δ AOD and Δ BOC

AD = BC [From (i)]

∠OBC =∠OAD (AD||BC and AB is transversal)

∠OCB =∠ODA (AD||BC and CD is transversal)

Therefore, by ASA theorem:

Δ AOD ≅ Δ BOC

OA = OB (By c.p.c.t)

And,

OD = OC (By c.p.c.t)

Hence, AB and CD bisect each other at O.