Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ACB = 90° and AC = 15 cm.
In right ∆ACB using pythagorous theorem:
(AB)2 = (AC)2 + (BC)2
(17)2 = (15)2 + (BC)2
BC = 8 cm
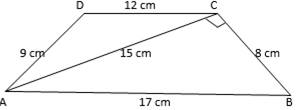
Perimeter of quad ABCD = AB+BC+CD+DA = 17+8+12+9 = 46 cm
Area of right angled ∆ACB = 
⇒ 
= 60 cm2
Now in equilateral ∆ACD
Let a, b and c are the sides of triangle and s is
the semi-perimeter, then its area is given by:
A = 
where 
[Heron’s Formula]
=
= 18
A= 
A = 
= 
cm2
Hence, area of quad ABCD =60+54 =114 cm2
10