Simplify each of the following products:

(i)

(ii)

(iii) -x² + 2x

(iv) (x² + x – 2) (x² - x + 2)

(v) (x³ - 3x² – x) (x² - 3x + 1)

(vi) (2x⁴ - 4x² + 1) (2x⁴ - 4x² - 1)

(i) On regarranging we get,

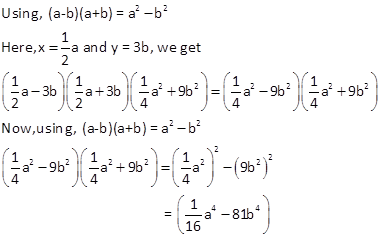
(ii) On regarranging we get,

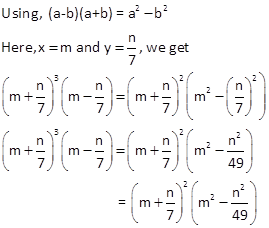
(iii) On rearranging we get, -x² + 2x

=

Using, (a-b)² = a² + b² – 2ab

(iv) Using the idendity, (a+b)(a-b) = a²-b²

On rearranging we get,

(x² + x – 2) (x² - x + 2) = {x² + (x – 2)} {(x² – (x - 2)}

= (x²)² – (x – 2)² = x⁴-(x² - 4x + 4)

= x⁴ – x² + 4x – 4

(v) Taking x as common factor, we write,

= x (x² - 3x – 1) (x² - 3x + 1)

= {x (x² - 3x – 1)} (x² - 3x + 1)

= x [{(x² - 3x) – 1)} {(x² - 3x)+1)}]

= x {(x² - 3x)² – 1²}

= x (x⁴ - 6x³+9x²-1)

= x⁵ – 6x⁴ + 9x³ -x

(vi) On Reaaranging we get,

(2x⁴ - 4x² + 1) (2x⁴ - 4x² - 1)

= {(2x⁴ - 4x²) + 1} {(2x⁴ - 4x²)- 1)}

= (2x⁴ - 4x²)² – 1²

= 4x⁸ + 16x⁴ -2 × 2x⁴ × 4x² – 1

= 4x⁸ + 16x⁴ -16x⁶ -1