In a , D and E are points on the sides AB and AC respectively. For each of the following cases show that : (i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm. (ii) AB = 5.6 cm, AD = 1.4 cm, AE = 7.2 cm and AC = 1.8 cm. (iii) AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm. (iv) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.

Question

Philoid · Accepted Answer

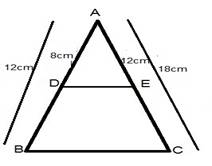
(i) AB = 12 cm, AD = 8 cm, and AC = 18 cm.

∴ DB=AB-AD

= 12-8

=4 cm

EC=AC-AE

= 18-12

= 6 cm

Now AD/DB=8/4=2

AE/EC=12/6=2

Thus DE divides side AB and AC of ⊿ ABC in same ratio

Then by the converse of basic proportionality theorem.

(ii)

AB = 5.6 cm, AD = 1.4 cm, AE = 1.8 cm and AC = 7.2 cm

∴ DB=AB-AD

DB=5.6-1.4

DB= 4.2 cm

And EC=AC-AE

EC= 7.2-1.8

EC=5.4

Now AD/DB=1.4/4.2=1/3

AE/EC=1.8/5.4=1/3

Thus DE divides side AB and AC of ⊿ ABC in same ratio

Then by the converse of basic proportionality theorem.

(iii)

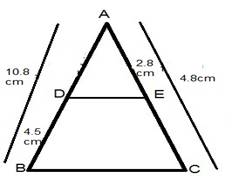
we have

AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm

∴ AD=AB-DB

AD=10.8-4.5

AD= 6.3 cm

And EC=AC-AE

EC= 4.8-2.8

EC=2 cm

Now AD/DB=6.3/4.5=7/5

AE/EC=2.8/2=28/20=7/5

Thus DE divides side AB and AC of ⊿ ABC in same ratio

Then by the converse of basic proportionality theorem.

(iv)

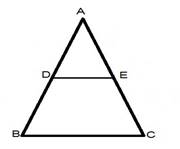
DE∥BC

We have,

AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm

Now AD/DB=5.7/9.5=57/95 =3/5

AE/EC=3.3/5.5=33/55=3/5

Thus DE divides side AB and AC of ⊿ ABC in same ratio

Then by the converse of basic proportionality theorem.