In Fig. 4.177, ![]() . If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. Also, find the area (
. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. Also, find the area (![]() ) : area (
) : area (![]() ).
).
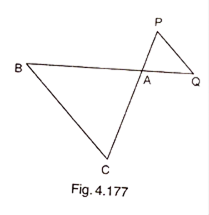
We have,
ΔACB ~ ΔAPQ
Then, AC/AP = CB/PQ = AB/AQ[Corresponding parts of similar Δ are proportional]
Or, AC/2.8 = 10/5 = 6.5/AQ
Or, AC/2.8 = 10/5 and 10/5 = 6.5/AQ
Or, AC = 5.6cm and AQ = 3.25cm
By area of similar triangle theorem
Area of ΔACB/Area of ΔAPQ = BC2 /PQ2
= (10)2/(5)2
= 100/25
= 4 cm
2