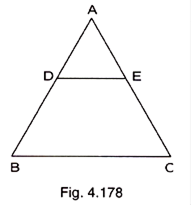
In Fig. 4.178,

(i) If DE = 4 cm, BC = 6 cm and area () = 16 cm², find the area of .

(ii) If DE = 4 cm, BC = 8 cm and area () = 25 cm², find the area of .

(iii) If DE : BC = 3 : 5. Calculate the ratio of the areas of and the trapezium BCED.

(i) We have , DE||BC, DE = 4cm, BC = 6cm and area (ΔADE) = 16cm²

In ΔADE and ΔABC

<A = <A (Common)

<ADE = <ABC (Corresponding angles)

Then, ΔADE ~ ΔABC (BY AA similarity)

So, By area of similar triangle theorem

Area of ΔADE/Area of ΔABC = DE² /BC²

16/Area of ΔABC = 4²/6²

Or, Area (ΔABC) = 16 x 36/16

= 36cm²

(ii) We have , DE||BC, DE = 4cm, BC = 8cm and area (ΔADE) = 25cm²

In ΔADE and ΔABC

<A = <A (Common)

<ADE = <ABC (Corresponding angles)

Then, ΔADE ~ ΔABC (BY AA similarity)

So, By area of similar triangle theorem

Area of ΔADE/Area of ΔABC = DE² /BC²

25/Area of ΔABC = 4²/8²

Or, Area (ΔABC) = 25 x 64/16

= 100 cm²

(iii) We have DE||BC, And DE/BC = 3/5 ……………(i)

In ΔADE and ΔABC

<A = <A (Common)

<ADE = <ABC (Corresponding angles)

Then, ΔADE ~ ΔABC (BY AA similarity)

So, By area of similar triangle theorem

Area of ΔADE/Area of ΔABC = DE² /BC²

Area of ΔADE/Area of ΔADE + Area of trap. DECB = 3²/5²

Or, 25 area ΔADE = 9 Area of ΔADE +9 Area of trap. DECB

Or 25 area ΔADE - 9 Area of ΔADE = 9 Area of trap. DECB

Or, 16 area ΔADE = 9 Area of trap. DECB

Or, area ΔADE / Area of trap. DECB = 9/16