ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 m, prove that area of ![]() is one-sixteenth of the area of
is one-sixteenth of the area of ![]() .
.
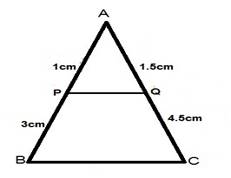
AP=1 cm, PB=3 cm,AQ=1.5cm,and QC=4.5 m
In ![]() APQ and
APQ and ![]() ABC
ABC
∠A=∠A [Common]
AP/AB=AQ/AC [Each equal to 1/4]
![]() APQ
APQ![]() ABC [By SAS]
ABC [By SAS]
By area of similar triangle theorem
Area (![]() ) =12
) =12
Area (![]() ) 42
) 42
Area (![]() ) =1
) =1
Area (![]() ) 16 x ar(
) 16 x ar(![]() )
)
19