AD is and altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area () : Area () = 3 : 4.

Question

AD is and altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( ) : Area ( ) = 3 : 4.

Philoid · Accepted Answer

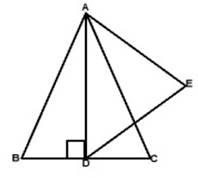
We have,

ABC is an equilateral triangle

AB=BC=AC=2X

∵ AD⊥BC then BD=DC=x

In ADB

AB²=(2x)²-(x)²=3x²

AD= cm

ABC and ADE both are equilateral triangles

∴ABCADE [By AA similarity]

By area of similar triangle theorem

Area() =AD² Area () AB²

Area() Area ()=()²/4x²

Area() Area () =3/4

Area()

Area () =3:4