A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flag-staff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.

Question

Philoid · Accepted Answer

Let the height of tower = h (m)

Let the height of the flag-staff = t (m)

In ∆DBC,

tan 45° =

1 =

h = 70 m

Therefore height of tower = 70m.

Now in ∆ABC,

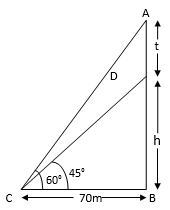
tan 60° =

√3 = ⇒ √3 = (on substituting value of h =70)

70+t = 70√3

t = 70√3-70

t = 70 (√3 -1)

t = 70 × (1.732-1)

t = 70 × 0.732 ⇒ 51.24 m.

Therefore height of the flag- staff is 51.24 m.