A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
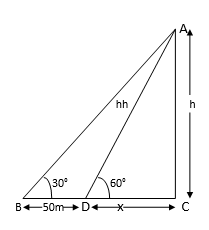
Let the height of the tower = h (m)
In ∆ABD,
tan 60° = 
√3 = 
h = 
---------- (1)
In ∆ABC,
tan 30° = 
tan 30° = 
------(2)
on substituting value of h from equn. (1) In equn. (2)
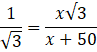
On cross multiplication
√3×√3
= 
3
= 
3
2
⇒ 25 m.
Now substituting value of 
in eqn. (1)
h = 25√3 ⇒ 43.3m.
Therefore height of tower is 43.3 m.
11