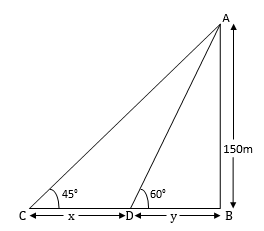
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.

Question

Philoid · Accepted Answer

Let the distance between the objects = (m.)

In ∆ABC,

tan 45° =

1 = ⇒

1 =

= 150 ----------(1)

In ∆ABD,

tan 60° =

√3 =

= 150

= -------(2)

substituting value of y in eqn.(1)

=

= ⇒ ⇒

=

= 63.4 m.

Therefore the distance between the points is 63.4 m.