The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from the point A.
Let the height of the tower is = h (m)
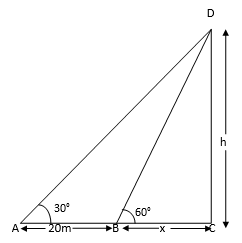
Distance of point B from foot of the tower is = 
(m)
In ∆ADC,
tan 30° = 
= 
√3 h = 20+
-----------(1)
In ∆DCB,
tan 60° = 
√3 = 
h = √3
----------(2)
On substituting value of h from eqn. (2) in eqn. (1)
√3× √3 
= 20 +
3
20+
3
-
= 20
= 10
Therefore distance of point A from tower is
AC = AB+BC
AC = 20+10 ⇒ 30
Ac = 30 m.
Now substituting value of 
in eqn. (1)
h = 20+10 ⇒ 30
⇒ 17.32 m.
Therefore height of tower is 17.32 m.
16