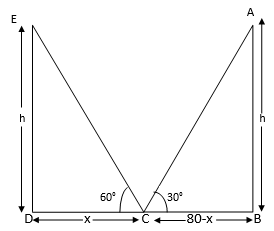
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.

Let AB and ED are two poles of equal height.

Let C be the point of elevation on the ground.

In ∆EDC

tan 60° =

h = √3 --------(1)

In ∆ABC

tan 30° =

√3h = 80-----------(2)

On substituting value of h from eqn.(1) in eqn. (2)

√3

3

4 = 80

On substituting value of in eqn. (1)

√3h = 80-20⇒ 60

h = ⇒ ⇒

h = 20√3 m.

Therefore height of poles is 20√3 m. and distances of the points from one pole is 20 m. and from other pole is 80-20 = 60 m.