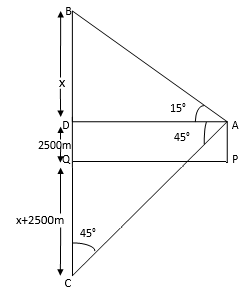
The angle of elevation of a stationery cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)

Question

Philoid · Accepted Answer

In the fig B is the position of the cloud and C is the point of reflection of the cloud in the lake.

In the fig BD = x

DQ = AP= 2500m

QC = BQ = BD + DQ = (2500 + x)m

DC = DQ +QC = 2500 + 2500 + x = (5000 + x)m

In ∆QRT

tan 45° =

1 =

AD = 5000 + x …………….(1)

Tan15° = tan (45° - 30°) = [Using formula tan(α-β) = ]

Tan15° = =

In ∆ABD

tan 15° =

=

(√3+1)x = (√3+1)(5000+x)

√3x + x = 5000√3 + √3x – 5000 - x

2x = 5000(√3-1)

x = 2500(√3-1)m

Now BQ = BD + DQ = x + 2500

(On substituting value of x)

BQ = 2500(√3-1) + 2500

⇒ 2500√3 – 2500 + 2500

2500√3m

Therefore height of cloud is 2500√3m