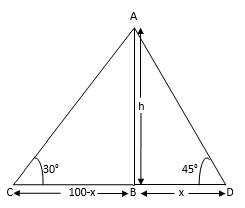
Two boats approach a light house in mid-sea from opposite directions. The angles of elevation of the top of the light house from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the light house.

In the fig AB is the light house of height h (m)

In ∆ABC

tan 30° =

=

x = 100 - √3 h ……………(1)

In ∆ABD

tan 45° =

1=

x = h …………(2)

On substituting value of x from eqn (2) in eqn (1)

h = 100 - √3 h

h + √3 h = 100

h (1 + √3) = 100

h = = ⇒ 50 (√3 - 1)

Therefore height of the light house is 50 (√3 - 1)m