The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the light house.

In the fig let AB is the light house of height h (m)

In ∆ABC

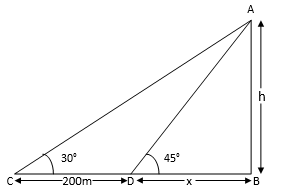
tan 30° =

=

√3h = 200 + x ………………….(1)

In ∆ABD

tan 45° =

1 =

h = x ………………(2)

From eqn (1) and (2) we get

√3h = 200 + h

h(√3 + 1) = 200

h =

On multiplying and dividing by √3-1, we get

h =

h = ⇒ 273.2m

Therefore height of the light house is 273.2m