An aeroplane is flying at a height of 210 m. Flying at this height at some instant the angles of depression of two points in a line in opposite directions on both the banks of the river are 45° and 60°. Find the width of the river.

In the fig AD is the position of the aeroplane. Let the width of the river is DC = DB + BC

In ∆ABD

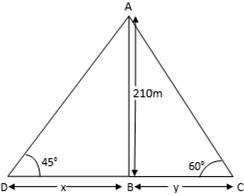
tan 45° =

1 =

x = 210m …………………(1)

In ∆ABC

tan 60° =

√3 =

√3y = 210

y =

On multiplying and dividing by √3, we get

y = ⇒ = 70√3 ……………………(2)

Therefore width of the river is = 210 +70√3 = 331.24m