The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.

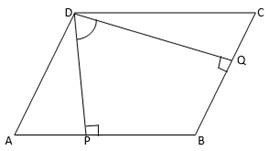
Given ABCD is a parallelogram in which DP⊥AB and AQ ⊥BC.
Given ∠PDQ = 60°
In quad. DPBQ
∠PDQ + ∠DPB + ∠B + ∠BQD = 360° [Sum of all the angles of a Quad is 360°]
60° + 90° + ∠B + 90° = 360°
∠B = 360° – 240°
Therefore, ∠B = 120°
But ∠B = ∠D = 120° [Opposite angles of parallelogram are equal]
∠B + ∠C = 180° [Sum of adjacent interior angles in a parallelogram is 180°]
120° + ∠C = 180°
∠C = 180° – 120° = 60°
Therefore, ∠A = ∠C = 70° (Opposite angles of parallelogram are equal)