In a parallelogram ABCD, AB = 10cm, AD = 6 cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find the length CF.

Question

In a parallelogram ABCD, AB = 10cm, AD = 6 cm. The bisector of &#x2220; A meets DC in E, AE and BC produced meet at F. Find the length CF.

Philoid · Accepted Answer

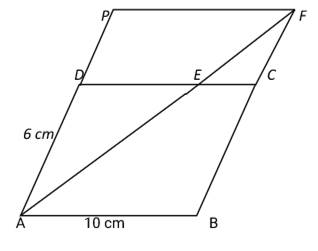
In a parallelogram ABCD

AB = 10 cm, AD = 6 cm
⇒ DC = AB = 10 cm and AD = BC = 6 cm [In a parallelogram opposite sides are equal]
Given that bisector of ∠A intersects DE at E and BC produced at F.
Draw PF || CD
From the figure, CD || FP and CF || DP
Hence PDCF is a parallelogram. [Since one pair of opposite sides are equal and parallel]
AB || FP and AP || BF
⇒ ABFP is also a parallelogram
Consider ΔAPF and ΔABF
∠APF = ∠ABF [Since opposite angles of a parallelogram are equal]
AF = AF (Common side)
∠PAF = ∠AFB (Alternate angles)
ΔAPF ≅ ΔABF (By ASA congruence criterion)
⇒ AB = AP (CPCT)
⇒ AB = AD + DP
= AD + CF [Since DCFP is a parallelogram]
∴ CF = AB – AD
CF = (10 – 6) cm = 4 cm