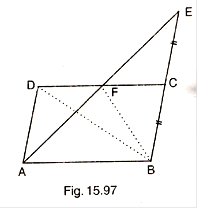
ABCD is a parallelogram in which BC is produced to E such that CE=BC. AE intersects CD at F.
(i) Prove that ar(Δ ADF) = ar(Δ ECF)

(ii) If the area of Δ DFB=3 cm², find the area of ||^gm ABCD.

Question

Philoid · Accepted Answer

In ADF and ECF

We have,

∠ADF = ∠ECF

AD = EC

And,

∠DFA = ∠CFA

So, by AAS congruence rule,

Δ ADF ≅ Δ ECF

Area (ΔADF) = Area (ΔECF)

DF = CF

BF is a median in ΔBCD

Area (ΔBCD) = 2 Area (ΔBDF)

Area (ΔBCD) = 2 * 3

= 6cm²

Hence, Area of parallelogram ABCD = 2 Area (ΔBCD)

= 2 * 6

= 12 cm²

ABCD is a parallelogram in which BC is produced to E such that CE=BC. AE intersects CD at F.(i) Prove that ar(Δ ADF) = ar(Δ ECF)(ii) If the area of Δ DFB=3 cm2, find the area of ||gm ABCD.