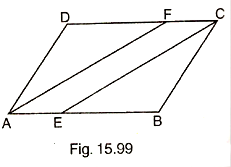
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC, such that DF=2FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram ABCD.

Question

Philoid · Accepted Answer

Construction: Draw FG perpendicular to AB

Proof: We have,

BE = 2 EA

And,

DF = 2FC

AB - AE =2 AE

And,

DC - FC = 2 FC

AB = 3 AE

And,

DC = 3 FC

AE = AB and FC = DC (i)

But,

AB = DC

Then,

AE = FC (Opposite sides of a parallelogram)

Thus,

AE || FC such that AE = FC

Then,

AECF is a parallelogram

Now, Area of parallelogram (AECF) = (AB * FG) [From (i)

3 Area of parallelogram AECF = AB * FG (ii)

And,

Area of parallelogram ABCD = AB * FG (iii)

Compare equation (ii) and (iii), we get

3 Area of parallelogram AECF = Area of parallelogram ABCD

Area of parallelogram AECF = Area of parallelogram ABCD

Hence, proved