In Fig. 15.83, CD||AE and CY||BA.

(i) Name a triangle equal in area of Δ CBX

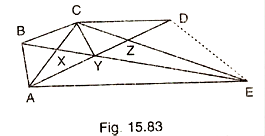
(ii) Prove that ar(Δ ZDE) = ar(Δ CZA)

(iii) Prove that ar(Δ BCYZ) = ar(Δ EDZ)

(i) ΔAYC and Δ BCY are on the same base CY and between the same parallels

CY || AB

Area (ΔAYC) = Area (ΔBCY)

(Triangles on the same base and between the same parallels are equal in area)

Subtracting ΔCXY from both sides we get,

Area (ΔAYC) – Area (ΔCXY) = Area (ΔBCY) – Area (ΔCXY) (Equals subtracted from equals are equals)

Area (ΔCBX) = Area (ΔAXY)

(ii) Since, ΔACC and ΔADE are on the same base AF and between the same parallels

CD || AF

Then,

Area ( = Area ()

Area () + Area ( = Area () + Area (

Area ( = Area () (i)

(iii) Since, ΔCBY and ΔCAY are on the same base CY and between the same parallels

CY || BA

Then,

Area () = Area ()

Adding Area ( on both sides we get

Area ( + Area ( = Area ( + Area ()

Area ( = Area ( (ii)

Compare (i) and (ii), we get

Area ( = Area (