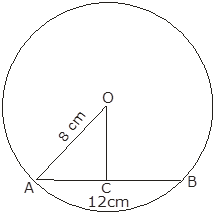
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.

Given that,

Radius of circle (OA) = 8 cm

Chord (AB) = 12 cm

Draw OC perpendicular to AB

We know that,

The perpendicular from centre to chord bisects the chord

Therefore,

AC = BC =

= 6 cm

Now,

In , by using Pythagoras theorem

AC² + OC² = OA²

6² + OC² = 8²

36 + OC² = 64

OC² = 64 – 36

OC² = 28

OC = 5.291 cm