Find the points of trisection of the line segment joining the points:

(i) (5, -6) and (- 7, 5), (ii) (3, -2) and (-3, -4), (iii) (2, -2) and (-7, 4)

(i) (5, -6) and (- 7, 5),

Let our given points be A(5,-6) and B(-7, 5) and required points be C (x₁ , y₁ ) and D(x₂ , y₂)

The points of trisection of a line are points which divide into the ratio 1:2

By section formula,

x = , y =

For point C(x₁ , y₁ )

x₁ = , y₁= …Here m = 1 and n = 2

∴ x₁ = , y₁ =

∴ C (x₁ , y₁ ) ≡ (1, )

For point D(x₂ , y₂ )

X₂ = , y₂= …Here m = 2 and n = 1

∴ x₂ = , y₂ =

∴ D (x₂ , y₂)≡ (-3, )

Hence, the points of trisection of line joining given points are (1, ) and (-3, )

(ii) (3, -2) and (-3, -4)

Let our given points be A(3,-2) and B(-3, -4) and required points be C (x₁ , y₁ ) and D(x₂ , y₂)

The points of trisection of a line are points which divide into the ratio 1:2

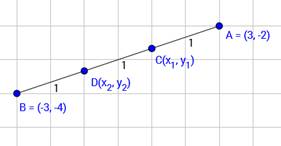
By section formula,

x = , y =

For point C(x₁ , y₁ )

x₁ = , y₁= …Here m = 1 and n = 2

∴ x₁ = , y₁ =

∴ C (x₁ , y₁ ) ≡ ( , )

For point D(x₂ , y₂ )

X₂ = , y₂= …Here m = 2 and n = 1

∴ x₂ = , y₂ =

∴ D (x₂ , y₂)≡ (-1, )

Hence, the points of trisection of line joining given points are ( , ) and (-1, )

(iii) (2, -2) and (-7, 4)

Let our given points be A(2,-2) and B(-7, 4) and required points be C (x₁ , y₁ ) and D(x₂ , y₂)

The points of trisection of a line are points which divide into the ratio 1:2

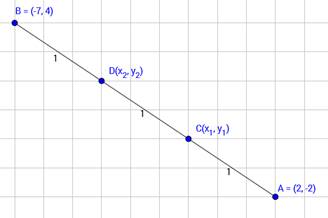
By section formula,

x = , y =

For point C(x₁ , y₁ )

x₁ = , y₁= …Here m = 1 and n = 2

∴ x₁ = , y₁ =

∴ C (x₁ , y₁ ) ≡ ( , )

For point D(x₂ , y₂ )

X₂ = , y₂= …Here m = 2 and n = 1

∴ x₂ = , y₂ =

∴ D (x₂ , y₂)≡ (-4, 2)