Determine the ratio in which the straight line x - y - 2 = 0 divides the line segment joining (3, -1) and (8, 9).

Let point be A(3, -1) and B(8, 9).

Let the line divide the line joining the points A and B in the ratio m:n at any point C(x, y)

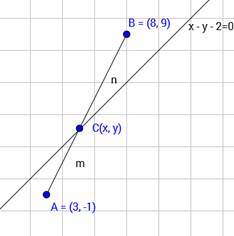
By section formula,

x = , y =

For point C(x, y),

x = , y =

∴ x = , y =

Now, substituting value of x and y in equation x - y - 2 = 0,

- -2 = 0

= 0

∴ -3m +2n =0

∴ =

∴ m:n = 2:3

Hence, the line divides the line segment joining A and B in the ratio 2:3 internally.