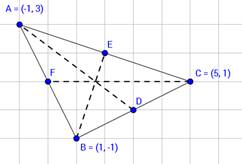
Find the lengths of the medians of a triangle whose vertices are A (-1,3), B (1,-1) and C(5,1).

Question

Philoid · Accepted Answer

Here given vertices are A(-1,3), B (1,-1) and C(5,1) and let midpoints of BC, CA and AB be D,E and F respectively.

By midpoint formula.

x = , y =

For midpoint D of side BC,

x = , y =

∴midpoint of side BC is D(3, 0)

For midpoint E of side AB,

x = , y =

∴midpoint of side AB is E(2, 2)

For midpoint F of side CA,

x = , y =

∴midpoint of side CA is F(0, 1)

By distance formula,

XY =

For median AD,

AD =

=

= 5 units

For median BE,

BE =

=

= units.

For median CF,

CF =

=

= 5 units