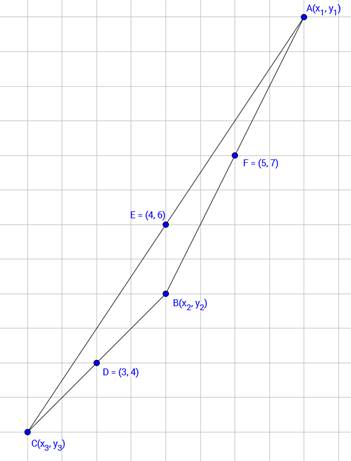
If the coordinates of the mid-points of the sides of a triangle are (3, 4), (4, 6) and (5, 7), find its vertices.
Let A(x1 , y1), B(x2 , y2) and C(x3 , y3) be the vertices of triangle.
Let D(3, 4), E(4, 6) and F(5, 7) be the midpoints of sides BC, CA and AB respectively.
By midpoint formula.
x = 
, y = 
For midpoint D(3, 4) of side BC,
3 = 
, 4 = 
∴ 
= 6 and 
= 8 …(1)
For midpoint E(4, 6) of side CA,
4 = 
, 6 = 
∴ 
= 8 and 
= 12 …(2)
For midpoint F(5, 7) of side AB,
5 = 
, 7 = 
∴ 
= 10 and 
= 14 …(3)
Adding 1,2 and 3, we get,
=6 + 8 + 10
And 
= 8 + 12 + 14
∴ 2(
= 24 and 2(
) = 34
∴ 
= 12 and 
= 17
+ 6 = 12 and 
+ 8 = 17 …from 1
∴ 
= 6 and 
= 9
Substituting above values in 3,
6 + 
and 9 + 
= 14
∴ 
= 4 and 
= 5
Similarly for equation 2,
6 + 
= 8 and 9 + 
= 12
∴ 
= 2 and 
= 3
Hence the vertices of triangle are A(6 , 9), B(4 ,5) and C(2 ,3)