Show that the points A (1, 0), B (5, 3), C (2, 7) and D (-2, 4) are the vertices of a parallelogram.

Let given points be A (1, 0), B (5, 3), C (2, 7) and D (-2, 4) and let the intersection of diagonals be E(x_m , y_m )

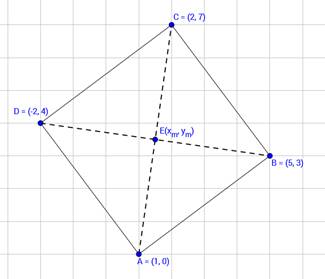
By midpoint formula.

x = , y =

For midpoint of diagonal AC,

X₁ = , y₁ =

∴x₁ = , y_{1 =}

∴ midpoint of diagonal AC is (x₁, y₁ ) ≡ (, ) …(1)

For midpoint of diagonal BD,

X₂ = , y₂ =

∴x₂ = , y ₂₌

∴ midpoint of diagonal BD is (x₂, y₂ ) ≡ (, ) …(2)

Here, from 1 and 2 we say that midpoint of both the diagonals intersect at same point, ie (, )

But our intersection of diagonals is at E, which means that midpoint of diagonals intersect at single point, ie E(, )

We know that if midpoints of diagonals intersect at single point, then quadrilateral formed by joining the points is parallelogram.

Hence, our □ABCD is parallelogram.