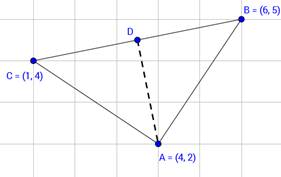
A (4, 2), B (6, 5) and C (1, 4) are the vertices of ABC.
(i) The median from A meets BC in D. Find the coordinates of the point D.

(ii) Find the coordinates of point P on AD such that AP : PD = 2 :1.

(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.

(iv) What do you observe?

Question

Philoid · Accepted Answer

(i) The median from A meets BC in D. Find the coordinates of the point D.

Here given vertices are A (4, 2), B (6, 5) and C (1, 4).

By midpoint formula.

x = , y =

For midpoint D of side BC,

x = , y =

Hence, the coordinates of D are ( , )

(ii) Find the coordinates of point P on AD such that AP : PD = 2 :1.

By section formula,

x = , y =

For point P on AD, where m = 2 and n = 1

x = , y =

∴ x = and y =

(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.

By midpoint formula.

x = , y =

For midpoint E of side AC,

x = , y =

Hence, the coordinates of E are ( , 3)

For midpoint F of side AB,

x = , y =

Hence, the coordinates of F are ( , )

By section formula,

x = , y =

For point Q on BE, where m = 2 and n = 1

x = , y =

∴ x = and y =

For point R on CF, where m = 2 and n = 1

x = , y =

∴ x = and y =

(iv) What do you observe?

We observe that the point P,Q and R coincides with the centroid.

This also shows that centroid divides the median in the ratio 2:1