If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.

Our given vertices are A(1, -2), B(3, 6) and C(5, 10) and fourth vertex be D(k, p)

It is given that quadrilateral joining these four vertices is parallelogram, ie □ABCD is parallelogram.

We know that diagonals of parallelogram bisect each other, ie midpoint of the diagonals coincide.

Let E(x_m , y_m) be the midpoint of diagonals AC and BD.

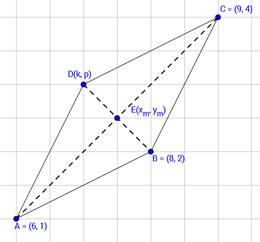
By midpoint formula,

x = , y =

For diagonal AC,

x_m = , y_m =

∴ x_m = , y_m =

∴ E(x_m , y_m) ≡ (, )

For diagonal BD,

= , =

∴ k = 15 – 8 , y = 5 – 2

∴ k = 7 and p = 3

Hence, our fourth vertex is D(7 , 3)