Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, - 6) and (-5, - 4)
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
(iii) (-4, - 2), (-3, - 5), (3, - 2), (2, 3)
(i) (-3, 2), (5, 4), (7, - 6) and (-5, - 4)
Let the vertices of the quadrilateral be A (−3, 2), B (5, 4), C (7, −6), and D (−5, −4). Join AC to form two triangles ∆ABC and ∆ACD.

Area of □ ABCD = Area of ∆ABC + Area of ∆ACD
Area of the triangle having vertices (x1,y1), (x2,y2) and (x3,y3)
= ![]() |x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
|x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
Area of ∆ABC
= ![]() |-3(4 – (-6))+5(-6 - 2)+7(2 - 4)|
|-3(4 – (-6))+5(-6 - 2)+7(2 - 4)|
= ![]() |-30 – 40 -14|
|-30 – 40 -14|
= 42 sq. units
Area of ∆ACD
= ![]() |-3(-6 – 4)+7(-4 - 2) - 5(2 + 6)|
|-3(-6 – 4)+7(-4 - 2) - 5(2 + 6)|
= ![]() |6 – 42 - 40|
|6 – 42 - 40|
= 38 sq. units
Area of □ ABCD = 42 + 38 = 80 sq. units
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ∆ABC and ∆ACD.
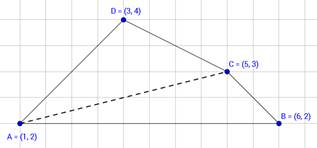
Area of □ ABCD = Area of ∆ABC + Area of ∆ACD
Area of the triangle having vertices (x1,y1), (x2,y2) and (x3,y3)
= ![]() |x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
|x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
Area of ∆ABC
= ![]() |1(2 – 3)+6(3 - 2)+5(2 - 2)|
|1(2 – 3)+6(3 - 2)+5(2 - 2)|
= ![]() |-1 + 6|
|-1 + 6|
= ![]() sq. units
sq. units
Area of ∆ACD
= ![]() |1(3 – 4)+5(4 - 2) + 3(2 - 3)|
|1(3 – 4)+5(4 - 2) + 3(2 - 3)|
= ![]() |-1 + 10 -3|
|-1 + 10 -3|
= 3 sq. units
Area of □ ABCD = ![]() + 3 =
+ 3 = ![]() sq. units
sq. units
(iii) (-4, - 2), (-3, - 5), (3, - 2), (2, 3)
Let the vertices of the quadrilateral be A (−4, −2), B (−3, −5), C (3, −2), and D (2, 3). Join AC to form two triangles ∆ABC and ∆ACD
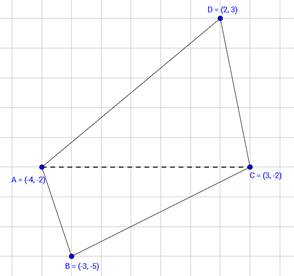
Area of □ ABCD = Area of ∆ABC + Area of ∆ACD
Area of the triangle having vertices (x1,y1), (x2,y2) and (x3,y3)
= ![]() |x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
|x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|
Area of ∆ABC
= ![]() |-4(-5 – (-2)) - 3(-2 – (-2)) + 3(-2 – (-5))|
|-4(-5 – (-2)) - 3(-2 – (-2)) + 3(-2 – (-5))|
= ![]() |12 + 0 +9|
|12 + 0 +9|
= ![]() sq. units
sq. units
Area of ∆ACD
= ![]() |-4(-2 – 3) - 3(3 – (-2)) + 2(-2 – (-2))|
|-4(-2 – 3) - 3(3 – (-2)) + 2(-2 – (-2))|
= ![]() |20 + 15 +0|
|20 + 15 +0|
= ![]() sq. units
sq. units
Area of □ ABCD = ![]() +
+ ![]() = 28 sq. units
= 28 sq. units