In the given figure, BA ⊥ AC and DE ⊥ EF such that BA=DE and BF=DC. Prove that AC=EF.

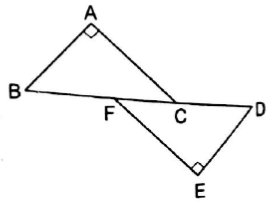
Given : BA ⊥ AC and DE ⊥ EF such that BA=DE and BF=DC

To prove: AC = EF

Proof:

In ∆ABC, we have,

BC = BF + FC

And , in ∆DEF,

FD = FC + CD

But, BF = CD

So, BC = BF + FC

And, FD = FC +BF

∴ BC = FD

So, in ∆ABC and ∆DEF, we have,

∠BAC = ∠DEF … given

BC = FD

AB = DE …given

Thus by Right angle - Hypotenuse- Side property of congruence, we have,

∆ABC ≅ ∆DEF

Hence, we know that, corresponding parts of the congruent triangles are equal

∴ AC = EF