In the given figure, OA=OB and OP=OQ. Prove that (i) PX=QX, (ii) AX=BX.

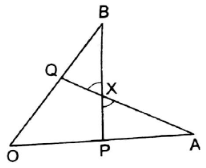
Given: OA=OB and OP=OQ

To prove: PX=QX and AX=BX

Proof:

In ∆OAQ and ∆OPB, we have

OA = OB …given

∠O = ∠O …common angle

OQ = OP … given

Thus by SAS property of congruence,

∆OAP ≅ ∆OPB

Hence, we know that, corresponding parts of the congruent triangles are equal

∠OBP = ∠OAQ …(1)

Thus, in ∆BXQ and ∆PXA, we have,

BQ = OB – OQ

And PA = OA – OP

But OP = OQ

And OA = OB …given

Hence, we have, BQ = PA …(2)

Now consider ∆BXQ and ∆PXA,

∠BXQ = ∠PXA … vertically opposite angles

∠OBP = ∠OAQ …from 1

BQ = PA … from 2

Thus by AAS property of congruence,

∆BXQ ≅ ∆PXA

Hence, we know that, corresponding parts of the congruent triangles are equal

∴ PX = QX

And AX = BX