In the adjoining figure, ABCD is a trapezium in which AB ‖ DC; AB = 7 cm; AD = BC = 5 cm and the distance between AB and DC is 4 cm. Find the length of DC and hence, find the area of trap. ABCD.


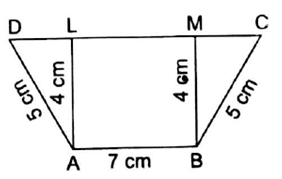
Given


AB = 7 cm


AD = BC 5 cm


AL = BM = 4cm (height)


DC = ?


Here in the given figure AB = LM


LM = 7 cm ------------1


Now Consider ALD


By Pythagoras theorem


AD2 = AL2 + DL2


52 = 42 + DL2


DL2 = 5 2 - 42 = 25 – 16 = 9


DL = 3 cm --------------2


Similarly in BMC


By Pythagoras theorem


BC2 = BM2 + MC2


52 = 42 + MC2


MC2 = 5 2 - 42 = 25 – 16 = 9


MC = 3 cm --3


from 1 2 and 3


DC = DL + LM + MC = 3 + 7 + 3 = 13 cm


We know that area of trapezium is x (sum of parallel sides) x height


Area of trapezium = x (AB + DC) x AL


= x (7 + 13) x 4 = 40 cm2


Area of trapezium ABCD = 180cm2

6
1