In the adjoining figure, D and E are points on the sides AB and AC of ∆ABC such that ar(∆BCE) = ar(∆BCD).

Show that DE ‖ BC.

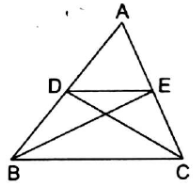
Given

A triangle ABC in which points D and E lie on AB and AC of ∆ABC such that ar(∆BCE) = ar(∆BCD).

To prove: DE ‖ BC

Proof:

Here, from the figure we know that BCE and BCD lie on same base BC and

It is given that area(∆BCE) = area(∆BCD)

Since two triangle have same base and same area they should equal altitude(height)

That means they lie between two parallel lines

That is DE ‖ BC

DE ‖ BC

Hence proved