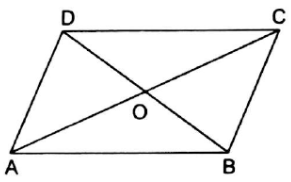
In the adjoining figure, O is any point inside a parallelogram ABCD. Prove that

(i) ar(∆OAB) + ar(∆OCD) = ar(‖gm ABCD),

(ii)ar(∆OAD) + ar(∆OBC) = ar(‖gm ABCD).

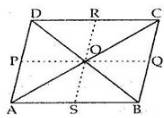
Given : A parallelogram ABCD with a point ‘O’ inside it.

To prove : (i) area(∆OAB) + area(∆OCD) = area(‖gm ABCD),

(ii)area(∆OAD) + area(∆OBC) = area(‖gm ABCD).

Construction : Draw PQ ‖ AB and RS ‖ AD

Proof:

(i)

∆AOB and parallelogram ABQP have same base AB and lie between parallel lines AB and PQ.

According to theorem: If a triangle and parallelogram are on the same base and between the same

parallel lines, then the area of the triangle is equal to half of the area of the parallelogram.

area(∆AOB) = area(‖gm ABQP) –--1

Similarly, we can prove that area(∆COD) = area(‖gm PQCD) –--2

Adding –1 and –2 we get,

area(∆AOB) + area(∆COD) = area(‖gm ABQP) + area(‖gm PQCD)

area(∆AOB) + area(∆COD) = = area(‖gm ABCD)

area(∆AOB) + area(∆COD) = area(‖gm ABCD)

Hence proved

(ii)

∆OAD and parallelogram ASRD have same base AD and lie between parallel lines AD and RS.

According to theorem: If a triangle and parallelogram are on the same base and between the same

parallel lines, then the area of the triangle is equal to half of the area of the parallelogram.

area(∆OAD) = area(‖gm ASRD) –--1

Similarly, we can prove that area(∆OBC) = area(‖gm BCRS) –--2

Adding –1 and –2 we get,

area(∆OAD) + area(∆OBC) = area(‖gm ASRD) + area(‖gm BCRS)

area(∆OAD) + area(∆OBC) = = area(‖gm ABCD)

area(∆OAD) + area(∆OBC) = area(‖gm ABCD)

Hence proved