In the adjoining figure, ∆ABC and ∆DBC are on the same base BC with A and D on opposite sides of BC such that ar(∆ABC) = ar(∆DBC).

Show that BC bisects AD.

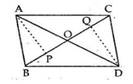
Given : ∆ABC and ∆DBC having same base BC and area(∆ABC) = area(∆DBC).

To prove: OA = OD

Construction : Draw AP ⊥ BC and DQ ⊥ BC

Proof :

Here area of ∆ABC = x BC x AP and area of ∆ABC = x BC x DQ

since, area(∆ABC) = area(∆DBC)

x BC x AP = x BC x DQ

AP = DQ -------------- 1

Now in ∆AOP and ∆QOD, we have

APO = DQO = 90 and

AOP = DOQ [Vertically opposite angles]

AP = DQ [from 1]

Thus by AAS congruency

∆AOP ∆QOD [AAS]

Thus By corresponding parts of congruent triangles law [C.P.C.T]

OA = OD [C.P.C.T]

Hence BC bisects AD

Hence proved