Prove that a median divides a triangle into two triangles of equal area.

Question

Philoid · Accepted Answer

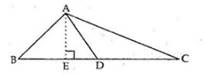
Given : A ∆ABC with D as median

To prove : Median D divides a triangle into two triangles of equal areas.

Constructions: Drop a perpendicular AE onto BC

Proof: Consider ∆ABD

area(∆ABD) = x BD x AE

Now , Consider ∆ACD

area(∆ACD) = x CD x AE

since D is the median

BD = CD

x BD x AE = x CD x AE

Hence , area(∆ABD) = area(∆ACD)

we can say that Median D divides a triangle into two triangles of equal areas.

Hence proved