The base BC of ∆ABC is divided at D such BD = ![]() DC. Prove that ar(∆ABD) =
DC. Prove that ar(∆ABD) = ![]() x ar(∆ABC).
x ar(∆ABC).
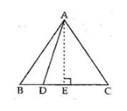
Given: A ∆ABC with a point D on BC such that BD = ![]() DC
DC
To prove: area(∆ABD) = ![]() x area(∆ABC)
x area(∆ABC)
Construction: Drop a perpendicular onto BC
Proof: area(∆ABC) = ![]() x BC x AE ---------------(1)
x BC x AE ---------------(1)
and, area(∆ABD) = ![]() x BD x AE ----------------- (2)
x BD x AE ----------------- (2)
given that BD = ![]() DC ------------------ (3)
DC ------------------ (3)
so, BC = BD + DC = BD + 2BD = 3BD [from 2]
∴ BD = ![]() (BC)
(BC)
Sub BD in (1), we get
area(∆ABD) = ![]() x (
x (![]() (BC) X AE)
(BC) X AE)
area(∆ABD) = ![]() x (
x (![]() BC X AE)
BC X AE)
![]() area(∆ABD) =
area(∆ABD) = ![]() x area(∆ABC) [from 1]
x area(∆ABC) [from 1]
Hence proved
25