In the given figure, is the center of a circle in which chords and intersect at such that bisects Prove that

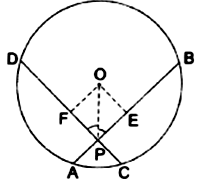
Proof

In ΔOEP and ΔOFP,

∠OEP = ∠OFP [equal to 90°]

OP = OP [common]

∠OPE = ∠OPF [OP bisects ∠BPD]

Therefore,

ΔOEP = ΔOFP [By angle-side-angle]

∴ OE = OF

AB = CD [Chords are equidistant from the center]

Hence, AB = CD Proved.