In the adjoining figure, is the center of a circle. If and are chords of the circle such that and prove that

Question

Philoid · Accepted Answer

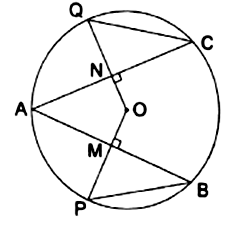
Given AB = AC

∴ (1/2)AB = (1/2)AC

OPAB and OQAC

∴ MB = NC

⇒ ∠PMB = ∠QNC [90°]

Equal chords are equidistant from the center.

⇒ OM = ON

OP = OQ

⇒ OP – OM = OQ – ON

⇒ PM = QN

∴ ΔABC ≅ ΔABC [By side-angle-side criterion of congruence]

∴ PB = QC Proved.