In the adjoining figure, is a square. A circle drawn with center cuts the suare in and Prove that

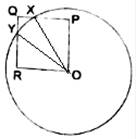
In triangle OPX and triangle ORY,

OX = OY [Radius]

∠OPX = ∠ORY [Common]

OP = OR [Sides of square]

By side-angle-side criterion of congruence,

ΔOPX ≅ ΔORY

∴ PX = RY

⇒ PQ – PX = QR – RY [PQ = QR]

⇒ QX = QY Proved.