In the adjoining figure, chords and of a circle with center intersect at right angles at If calculate

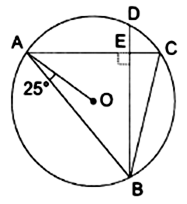
Join OB,

∴ OA = OB [Radius]

∴ ∠OAB = ∠OBA = 25°

In triangle AOB,

∠AOB + ∠OAB + ∠OBA = 180°[Sum of angles of triangle]

⇒ ∠AOB + 25° + 25° = 180°

⇒ ∠AOB + 50° = 180°

⇒ ∠AOB = 130°

Now,

∠ACB = (1/2) ∠AOB

⇒ ∠ACB = (1/2) 130°

⇒ ∠ACB = 65°

In triangle BEC,

∠EBC + ∠ECB + ∠BEC = 180°[Sum of angles of triangle]

⇒ ∠EBC + 65° + 90° = 180°

⇒ ∠EBC + 155° = 180°

⇒ ∠EBC = 25°