In the given figure, Show that is equal to the radius of the circumcircle of whose center is O.

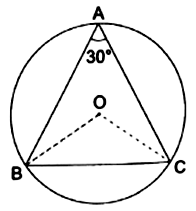
∠BOC = 2 × ∠BAC

⇒ ∠BOC = 2 × 30°

⇒ ∠BOC = 60°______________ (i)

OB = OC

∴ ∠OBC = ∠OCB ________________ (ii)

In triangle AOB,

∠OBC + ∠OCB + ∠BOC = 180°[Sum of angles of triangle]

⇒ 2 ∠OCB + 60° = 180°

⇒ 2 ∠OCB = 120°

⇒ ∠OCB = 60°

∴ ∠OBC = 60°[From equation (ii)]

From equation (i) and (ii),

∠OBC = ∠OCB = ∠BOC = 60°

∴ BOC is an equilateral triangle.

∴ OB = OC = BC

Hence, BC is the radius of the circumcircle.