is a rectangle. Prove that the center of the circle through is the point of intersection of its diagonals.

Question

Philoid · Accepted Answer

Let O be the point of intersection of the diagonals BD and AC of rectangle ABCD.

Since, the diagonals of a rectangle are equal and bisect each other.

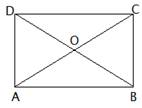
∴ OA = OB = OC = OD

Hence, O is the center of the circle through A, B, C, D.