In the given figure, is a quadrilateral in which and Show that the points lie on a circle.

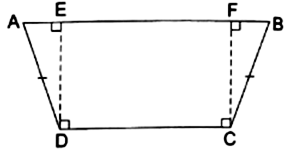
In ΔADE and ΔBCF,

AD = BC

∠AED = ∠BFC

∠ADE = ∠BCF [∠ADC - 90° = ∠BCD - 90°]

∴ ΔADE ≅ ΔBCF

The Cross ponding parts of the congruent triangles are equal.

∴ ∠A = ∠B

Now,

∠A + ∠B + ∠C + ∠D = 360°

⇒ 2 ∠B + 2 ∠D = 360°

⇒ ∠B + ∠D = 180°

∴ ABCD is a cyclic quadrilateral.