The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backwards, bisects the opposite side.

Given: Let ABCD be a cyclic quadrilateral, diagonals AC and BD intersect at O at right angles.

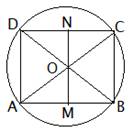
∠OCN = ∠OBM [Angles in the same segment] ___________ (i)

∠OBM + ∠BOM = 90° [Because ∠OLB = 90°] ______________ (ii)

∠BOM + ∠CON = 90°[LOM is a straight line and ∠BOC = 90°] ______________ (iii)

From equation (ii) and (iii),

∠OBM + ∠BOM = ∠BOM + ∠CON

⇒ ∠OBM = ∠CON

Thus, ∠OCN = ∠OBM and ∠OBM = ∠CON

⇒ ∠OCN = ∠CON

∴ON = CN ____________________ (iv)

Similarly, ON = ND ___________________ (v)

From equation (iv) and (v),

CN = ND Proved.